mstd()
Description:
Calculate the standard deviation on a matrix or a multidimensional matrix.
Syntax:
mstd(A, n)
Note:
An external library function (See External Library Guide) where parameter n is the sequence number of the level on which the summarization is performed. If n is absent, the desired dimension is the first one whose size is not 1 in matrix A.
Parameter:
|
A |
A matrix or a multidimensional matrix. |
|
n |
A positive integer. |
Option:
|
@s |
Perform the calculation using a statistical method, during which the n-1 is the divisor. |
|
@a |
Calculate the standard deviation on all elements of matrix A and parameter n is invalid. |
Return value:
Sequence/Number
Example:
|
|
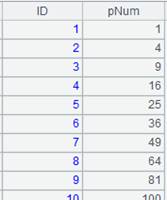
A |
|
||||
|
1 |
[[11,12,13],[21,22,23],[31,32,33]] |
|
||||
|
2 |
=mstd(A1,1) |
Calculate standard deviation on the matrix’s first level – that is, calculate standard deviation on members of each column. |
||||
|
3 |
=mstd(A1, 2) |
Calculate standard deviation on the matrix’s second level – that is, calculate standard deviation on members of each row. |
||||
|
4 |
=mstd(A1) |
Calculate standard deviation on the first level since parameter n is absent. |
||||
|
5 |
=mstd@a(A1) |
Calculate standard deviation on all elements of the matrix. |
||||
|
6 |
=mstd@s(A1) |
Perform the calculation using the statistical method.
|
||||
|
7 |
[[[111,112,113],[121,122,123],[131,132,133]],[[211,212,213],[221,222,223],[231,232,233]]] |
Define a three-dimension matrix whose two members are 3*3 matrices. |
||||
|
8 |
=mstd(A6, 1) |
Calculate standard deviation on matrix A6’s first level, that is, perform the calculation on both of its two member matrices in alignment. |
||||
|
9 |
=mstd(A6, 2) |
Calculate standard deviation on matrix A6’s second level, that is, perform the calculation on each column of each member matrix. |