Clustered files

After clustered servers are started, they can provide remote file service and remote cursor service, enabling users to access files stored on them.

10.2.1 Accessing a clustered file

Files on a clustered server are used in the same way as local files. For example:

	A
1	192.168.1.112:8281
2	PersonnelInfo_n1.txt
3	=file(A2,A1)
4	=A3.import@t()
5	=A4.derive().run(if(Gender=="M", Gender="Male"))
6	>A3.export@t(A5)
7	=A3.import@t()

Before executing the cellset, we need to place PersonnelInfo_n1.txt in the main path D:\files\node1 of the started clustererd server. We can directly copy the previously used PersonnelInfo.txt and rename it. If we need to use the file locally, remember not to set the same esProc main path as that on the clustered server. Suppose we use the following esProc main path in the local:

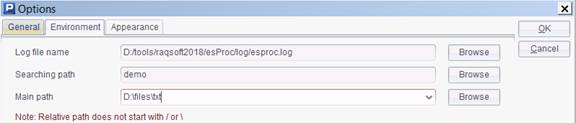
Then we execute the code and get the following result in A4:

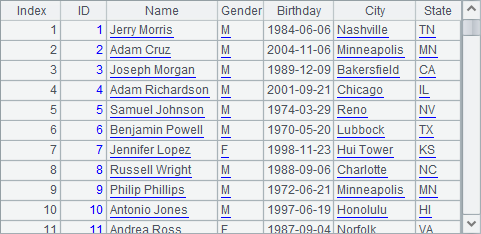
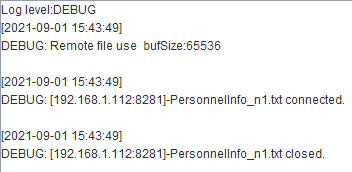
Similar to handling a local file, we can also use file(fn,h) function to read a composite table file fn from node list h and open a clustered file. The file, as a local file, can be saved in the main path or search path of the node. We can use file(fn:cs,h) function to specify a special character set through parameter cs as needed. Related information of using a clustered file will be recorded at esProc backend and will not be displayed in the file’s output window, as shown below:

A5 copies data in A4’s table and change Gender values of male employees to Male. A6 exports A5’s result to the clustered file. After A6 is executed, we view result in A7 as follows:

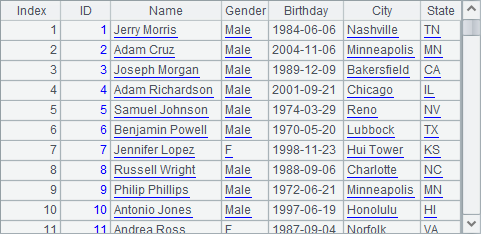
When we specify that we access a specific node to get a clustered file, the specified target will be accessed. The file is both readable and writable.

 

We can specify more than one node when tyring to use clustered files. The nodes to be used in one computer should first be configured in Config under Node Server, as shown below:

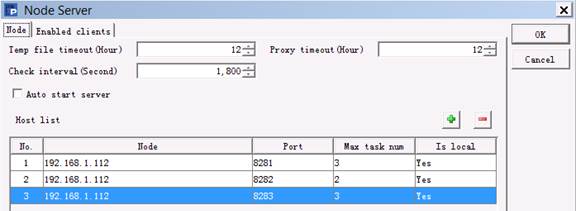
When a new clustered server is needed, the IP address and port number of an unstarted node in the node list will be used. In order to distinguish different nodes, we first set the main path D:\files\node2 before starting the second clustered server, as shown below:

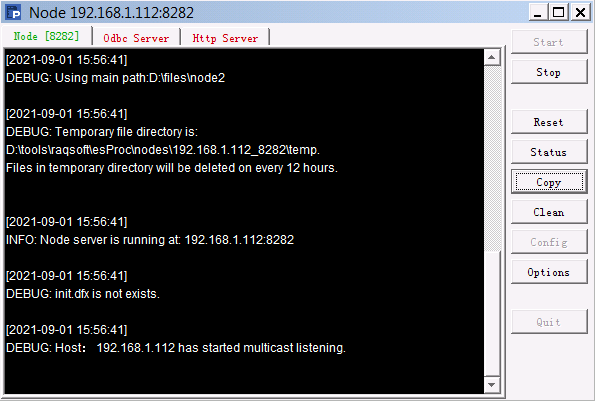
There are not any files in the second clustered server’s main path for the time being. In this case we specify a node list to get and use a clustered file, as shown below:

	A
1	[192.168.1.112:8281,192.168.1.112:8282]
2	PersonnelInfo_n1.txt
3	=file(A2,A1)
4	=A3.import@t()
5	=A3.cursor@t()
6	>A5.skip(90000)
7	=A5.fetch@x(5)

In order to specify multiple nodes, we use file(fn,hs) function to specify a node list hs. A4 returns result correctly, getting same data as A7 in the previous cellset. To access a clustered file through a node list, only one node containing the target file in its main path is sufficient for use.

A clustered file can be opened as a cursor for computation. In the above cellset file, A5 creates the cursor, and A7 fetches records from the 90001^th to the 90005^th. Below is A7’s result:

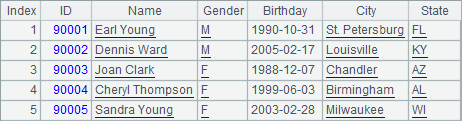
When using a clustered file by specifying a node list and in the meantime, there is a namesake file in local esProc’s main path, the local file is the first choice to use in the computation. In this case, the target clustered file is read-only since it could come from any of the node list or may come from the local machine.

10.2.2 Maintaining clustered files

We do not need to specifically access the main paths or search paths of clustered files on nodes in order to manipulate them. Instead, we handle them using functions, as shown below:

	A	B
1	192.168.1.112:8281	192.168.1.112:8282
2	PersonnelInfo.txt
3	PersonnelInfo_n1.txt	PersonnelInfo_n2.txt
4	=movefile@c(A2;"/",B1)	=movefile(A3,A1;"/",B1)
5	=movefile(A2,B1;B3)	=movefile@c(A2;"/",[A1:B1])
6	=movefile(A2;,[A1:B1])	=movefile@c(A3,B1;"/",A1)
7	=movefile(A3,A1;"/",B1)

This cellset file defines two nodes started in one computer. Node Ⅰ is 192.168.1.112:8281 and its main path is D:/files/node1. Node Ⅱ is 192.168.1.112:8282 and its main path is D:/files/node2. At the beginning, the main paths on the two nodes contain files as follows:

 

We execute the above code step by step. A4 uses movefile@c(fn; p, hs) function to copy local file fn into directory p on clustered server hs. The @c option enables a copy operation. Here only node Ⅱ is specified in the function to copy the target file to the node’s main path. After the code executed, the main paths on the two nodes contain files as follows:

 

A file is uploaded to the main path of node Ⅱ. The related information will be displayed to the clustered server’s output window:

B4 uses movefile(fn, h; p, hs) function to copy file fn on clustered server h into path p on clustered server hs. Here PersonnelInfo_n1.txt is moved from Node Ⅰ to Node Ⅱ’s main path. As no corresponding is used, the original file is deleted and directory D:/files/node1 becomes empty after the move operation is executed. Now there are files in directory D:/files/node2 as follows:

 

The two nodes’ system output windows display information as follows:

 

In A5, movefile(fn, h; p, hs) function does not specify the target node parameter hs, and file fn will be renamed p. In this case, p does not represent a target path any more, instead it is the new file name. Still, there are no files in directory D:/files/node1after execution, and D:/files/node2 has the following files:

 

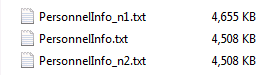
Similar to A4, B5 copies the local file PersonnelInfo.txt, but it uses a sequence to specify multilple target nodes, two which the file will be copied. After execution the main paths of the two nodes have the following files:

 

The two clustered servers’ system output windows display same information at file copy:

 

In A5, movefile(fn, h; p, hs) function does not specify the target path parameter p and thus, deletes the file. Below are the files in the main paths of the two nodes after execution:

 

Yet A5 specifies the target node parameter hs and, deletes the file from all involved nodes. In this case the node h holding the source file should be absent in order to avoid deleting the source file. If you specifies source node h but does not specify the target node parameter hs, the function will delete the file from the specified node.

The deletion operation information will be displayed in the two nodes’ output sytem windows. The two have same information as follows:

B6 copies PersonnelInfo_n1.txt on node Ⅱ to node Ⅰ. Now there are the following files in the main paths of the two nodes:

 

Now error occurs when A7 is trying to move PersonnelInfo_n1.txt from node Ⅰ to node Ⅱ:

 

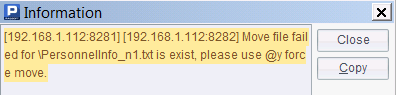
This is because there is already a namesake file in the target directory. To avoid the error and the incurred termination of execution, we use @y option in movefile() function to force overwriting a namesake file in the target path at file moving or copy.