Using Sequences

A sequence is an ordered set consisting of a series of data items, which are called members of the sequence. A sequence is similar to an array in high-level languages, but allows its members to be various data types. This part covers its basic uses from the aspects of creation, access, operators and functions.

2.4.1 Creation

Creating sequences with constants

To make the viewing convenient, esProc adds an Index column at the leftmost for each display of a sequence or a table sequence. The column isn’t a part of the table structure. Not all the screenshots of sequences or TSeqs in this Tutorial show the Index column.

Bracketing one or more constants with “[]” represents a sequence constant. Bracketing an expression with “[]” makes a sequence too. For example:

	A	B	C
1	1	red	2013-06-04
2	2	blue	27.49
3	3	yellow	Tom
4	[15.2,b,1]	=[A1:C3]	=[3,A4,B4]
5	[1,2,3,3]	[]	[[]]

In the cellset, A4, A5, B5 and C5 contain respectively a sequence constant. B4 and C4 contain sequences obtained by computing the expressions.

Members of the sequence in A4 are of various data types, including float, string and integer. Members in B4’s sequences are cell values defined by a range of cells. In C4, members of the sequence contain sequences. And there are identical members in A5’s sequence. The sequences in A4, B4, C4 and A5 respectively are as follows:

 

 

Let’s look at the values of B5 and C5:

 

You can see that the value of B5 is an empty sequence, while the value of C5 is a non-empty sequence, whose only member is an empty sequence.

Note: A member of a sequence can be of any data type, including one of the basic types, sequence, record, etc. A sequence whose all members are integers is called an integer sequence.

Creating sequences with functions

	A
1	=to(2,6)
2	="1,a,b,c".split@c()
3	=periods@y("2014-08-10",date(now()),1)
4	=file("sales.txt").import@t()

The code in A1 represents a sequence composed of the consecutive integers from 2 to 6; It can be abbreviated as to(6) if the sequence begins with 1. A2 splits a string to form a sequence. A3 creates a sequence of dates between two given dates according to the time unit of the year. The results of A1, A2 and A3 are as follows:

   

A4 imports records from a structured text file and creates a sequence. It’s value is as follows:

A sequence whose members are records is a table sequence, which is often used to perform structured data computing. Here the table sequence isn’t our focus. For more information, please refer to Operations on TSeqs and RSeqs.

Creating sequences by computation

In the following cellset, A1 imports the text file sales.txt as a table sequence; A2 retrieves STATE column and generate a sequence; A3 groups the records by STATE and generate a sequene:

	A
1	=file("sales.txt").import@t()
2	=A1.(STATE)
3	=A1.group(STATE)

After computation, the sequence in A2 is as follows:

The sequence in A3 is as follows:

It can be seen that each member of A3’s sequence is as sequence whose members are records.

2.4.2 Data access

Accessing members according to ordinal numbers

	A	B
1	[a,b,c,d,e,f,g]
2	=A1(2)	=A1.m(2)
3	=A1([2,3,4])	=A1(to(2,4))
4	=A1.m(-1)

The expressions in A2 and B2 are equal. Both of them fetch the second member from the sequence. The value is as follows:

A3 fetches members from the second to the fourth from the sequence, with the value being a sequence. Please note that [2,3,4] is also a sequence (integer sequence). The results of the expressions in B3 and A3 are the same:

A4 fetches the last member of the sequence. Note that A.m() function must be used when members are fetched backwards and the expression shouldn’t be abbreviated to A1(-1). A4’s result is as follows:

A.(m) function can be used to access multiple members. It also allows specify one or more intervals. For example:

	A	B
1	[a,b,c,d,e,f,g]
2	=A1.m(2,-2)	=A1.m(2:4,3:5)
3	=A1.m(-1,4:-2,5)	=A1.m(-2:2)

A2 get the second and the second-to-last members of the given sequence. B2 gets members by specifying two intervals. A3 gets members by specifying positions and an interval. Here are results of A2, B2 and A3:

  

The order of the starting position and ending position of the desired members in a specified interval should be in consistent with the normal order. A reverse order, like that of B3 where the interval is (-2:2) will produce a null result.

You can also use A.(to) function to access members of an interval in a given sequence. For example:

	A	B
1	[a,b,c,d,e,f,g]
2	=A1.to(2,4)	=A1.to(4,2)
3	=A1.to(3)	=A1.to(-3)

Here are results of A2, B2, A3 and B3:

 

 

According to B2’s result, different from A.(m) function, A.(to) function allows specifying members with an interval backward to forward. This way members of the resulting sequence is in a reverse order. A3 gets the first 3 members in the given sequence, and B3 gets the last three members.

Assignment and modification

	A
1	[a,b,c,d,e,f,g]
2	>A1(2)="r"
3	>A1([3,4])=["r","s"]
4	>A1.modify(4,[ "r","s"])

In order to clearly view the change that the statement in each cell introduces, click  on the tool bar to execute the code step by step.

A2 modifies the second member in A1 into r; A3 goes on to modify the third and fourth members in A1. A4 continues the modification from the fourth member in order. The expression in A4 equals >A1([4,5])=["r","s"]. With the step-by-step execution, the changes of sequence in A1 are shown as follows:

Adding members

	A
1	[a,b,c,d,e,f,g]
2	>A1.insert(0,"r")
3	>A1.insert(2,["r","s","t"])

A2 appends a new member at the end of the sequence. A3 continues to insert three members consecutively before the second member. When executed step by step, the sequence in A1 has undergone the following changes:

Besides insert function, you can use A.pad(x,n) function to add x continuously to the sequence A until the number of members of A reaches n. For example:

	A
1	[a,b,c,d,e,f,g]
2	=A1.pad("A",10)

When executed, A2’s result is as follows:

The pad function doesn’t affect the original sequence in A1.

Deleting members

	A
1	[a,b,c,d,e,f,g]
2	> A1.delete(2)
3	> A1.delete([2,4])

A2 deletes the second member. A3 continues to delete the second and the fourth members. When executed step by step, the sequence in A1 has experienced the following changes:

2.4.3 Operators

Set operations

Set operations include ^ (intersection), & (union), \ (difference), and | (concatenation), etc. For example:

	A	B
1	[a,b,1,2,3,4]	[d,b,10,12,3,4]
2	=A1^B1	=A1\B1
3	=A1&B1	=A1|B1

The sequences in A1 and B1 are as follows:

 

A2, B2, A3 and B3 compute respectively the intersection, difference, union and concatenation of the two sequences. After the computations are finished, the results of A2, B2, A3 and B3 are as follows:

 

 

Note: Both union and concatenation are created by combining members of two sequences in order. Their common members only appear once in union, while, in concatenation, all the duplicates will appear.

In the above set operations, a sequence has members of different data types, including string and integer. The binary operations only need to check whether members in the involving sequences are same or not, so the above code can execute normally. But a string and an integer can’t be compared to see which is bigger or smaller. To compare members, like what the sorting operation requires, the members of sequences must be comparable. For example:

	A	B	C
1	[3.456,5L,,2,-3,4]	=["d","b","Ace",,"Tom","3"]	[a,b,1,2,3,4]
2	=A1.sort@z()	=B1.sort()	=C1.sort()

Members of A1’s sequence include real numbers and a null. B1’s members are strings and a null. Members of both A1 and B1 are comparable. Below are the sorted sequences in A2 and B2:

 

The null is generally treated as the smallest value.

Members of C1’s sequence include both strings and integers. The two types of data can’t be compared, so an error is reported about C2 when being executed:

Alignment arithmetic operations

You can perform alignment operations on members of two sequences of the same length and return a sequence. The operation includes ++ (addition), -- (subtraction), ** (multiplication), // (division) and %% (Mod). For example:

	A	B
1	[1,2,3,4]	[10,12,3,4]
2	=A1++B1	=A1--B1
3	=A1**B1	=A1//B1

The sequences in A1 and B1 are as follows:

 

A2, B2, A3 and B3 perform addition, subtraction, multiplication and division respectively on the two sequences in alignment. After computation, the results of A2, B2, A3 and B3 are as follows:

 

 

Boolean operations

esProc offers cmp(A,B) funciton to compare the sizes of two sequences A and B.

Ø  cmp(A,B)

The function compares values of each pair of members at correponding positions in two sequences until the first pair of unequal members appears. If the value of the member in sequence A is greater than that of the member in sequence B, the function returns 1; if the former is less than the latter, it returns -1; and if they are equal, return 0. Note that cmp(A), or cmp(A,0), represents the comparison between sequence A and an integer sequence whose members are zeros, that is, cmp(A,[0,0,…,0]).

	A
1	=cmp(["a","b","c"],["a","b","c"])
2	=cmp([1,3,5,7],[1,3,7,5])
3	=cmp([7,6,5,4],[7,6,4,10,11])

Below are the results of A1, A2 and A3:

   

Two sequences can be compared in alignment. The result is boolean type. For example:

	A
1	=[1,2,3]==[1,2,3]
2	=[1,"B",3]<=[1,"b",4]
3	=[1,2,3]<[1,3,4]

The result of A1 is true, meaning the two sequences are equal. The result of A2 is true, because B is smaller than b. The result of A3 is true because 2, the second member of the first sequence, is smaller than 3, the second member of the second sequence:

   

Note: An esProc sequence is an ordered set. Order is critical in comparing two sequences A and B. To check if two sequences have the same members, use A.eq(B) function:

	A
1	[Tom,Jerry,Tuffe,Tyke]
2	[Jerry,Tuffe,Tom,Tyke]
3	=A1==A2
4	=A1.eq(A2)

Because the orders of the members in A1 and A2 are different, they are not equal, as shown by A3’s result:

A4’s true result means the seqences have same members:

2.4.4 Sequence-related functions

Sequence and string

esProc offers s.split() function and A.concat() function to switch between the sequence and the string. s.split(d) function splits string s to form a sequence with the dilimiter d, and identifies data types automatically if working with @p option. If d is omitted, split the string by characters. A.concat(d) function generates a string from sequence A with the dilimiter d, and it data types automatically. If d is omitted, use no dilimiter. Both funcitons can work with @c option to use the comma as the dilimiter. For example:

	A
1	a,1,c,2011-8-11,false
2	=A1.split@c()
3	=A2.concat@c()

Results of A2 and A3 are as follows:

 

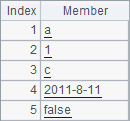
The resulting sequence of A2’s string splitting has string members. To automatically parse the data types, use @p option in the function.

The s.regex(rs) function matches string s with the regular expression rs and returns a sequence-type matching result, or null, if none of the characters in string s can be matched. The use of @c option in the function means case-insensitive, and an @u option makes the function perform matching according to Unicode.

The simplest use of the regex() function is to match the given regular expression with a certain string and get the result. The following example shows the way of matching up the numeric string:

	A	B	C
1	="a12b".regex("(a[0-9])")	="a12b".regex("(a[0-9]*)")	="a12b".regex("[0-9]b")
2	="a12b".regex("\\S*([0-9][a-z])")	'\S*([0-9][a-z])	="a12b".regex(B2)

Below are results of A1, B1 and C1:

  

For the regular expression "(a[0-9])" A1 uses, a matches a letter a, [0-9] matches any single-bit number from 0 to 9, and the parentheses () indicates finding a string “beginning with letter a that is followed by a single-bit number” and returning it. As is shown above, the result is a sequence with a single member a1. In B1’s regular expression, the asterisk * means matching the type of character preceding it, which is the number defined by [0-9] here, consecutively. So B1 returns a result of a12. C1 tries to find a string beginning with a number followed by letter b, but the string a12b isn’t one “headed by a number”; so the matching fails and C1 returns null.

In A2’s regular expression "\\S*([0-9][a-z])", [a-z] represents a character, i.e. any lower-case letter, from a to z; and \S* stands for any number of non-whitespace characters appearing in a row. Since the slash \ also means the escape character in a string, it needs to be escaped to be a literal – that is the \\S*. The parentheses specify that the returned substring should be the match of [0-9][a-z] while the match of \S* will be discarded. In B2, the regular expression is written as a string constant which doesn’t need to be escaped. C2 thus gets the same result as A2 does. Here’re results of A2 and C2:

 

esProc uses the parentheses () to define the substring to be returned when matching a string with the regular expression. The returned result is a sequence consisting of members defined by the parentheses. Without the parentheses, the substring itself will be returned if the matching is successful.

With the @c option, regex() function becomes case-insensitive when matching a string with the regular expression. For example:

	A	B	C
1	="a12b".regex@c("(A[0-9])")	="a12b".regex@c("([A-Z][0-9])")	="a12b".regex("([A-Z][0-9])")

Here’re results of A1, B1 and C1:

  

A1’s regular expression includes the uppercase letter A, and B1’s matches any uppercase letter. Both return a result of a1 because of the use of @c option. C1 returns null because the function works alone without the @c option and can’t find a match for the regular expression.

In short, the regex() function returns a sequence consisting of the matching result when the regular expression rs finds its match in string s; and null when it can’t find a match.

esProc allows using the universal unicode symbols to display non-English characters in the regular expression so that the character set setting can’t intervene. To do that, remember adding @u option to the regex() function. For example:

	A	B
1	="Gerente de Fábrica".regex(".* (.*á.*)")	="Gerente de Fábrica".regex@u(".* (.*\\u00e1.*)")

The regular expression .* (.*á.*) in A1 includes a dot (.) and .*. The dot represents any single character except carriage return and new line; .* represents any number of random characters. A1’s regular expression finds the last word substring containing the character á. So does B1’s. But the regex() function in B1 adds @u option to display the character á as \u00e1 according to Unicode. Usually the syntax of regex@u() is used to parse a string on the outside, keeping the regular expression from being affected by the character set setting. Both A1 and B1 get the same result:

 

Aggregate functions

Aggregate functions used to manipulate sequences include A.sum(),A.avg(), A.max(), A.min() and A.variance() etc., respectively for computing sum, average, maximum value, minimum value and variance. They have similar uses. Here’s an example:

	A
1	[2,4,6]
2	=A1.sum()
3	=A1.sum(~*~)

A2 computes the sum of the sequence’s members. A3 computes the sum of the members’ squares. Results of A2 and A3 are as follows:

 

If members of a sequence are boolean conditions, we can use A.cand() and A.cor() functions to judge whether all conditions are true or at least one of them is true. For example:

	A	B	C	D
1	=[1,2,3,4].cand(24%~==0)	=[12,-3,0].cor(24%~==0)	[]
2	for 500	=A2%3==2	=A2%5==3	=A2%7==2
3		if [B2:D2].cand()	>C1=C1|A2

A1 judges whether all members in sequence [1,2,3,4] are divisors of 24. B1 checks whether sequence [12,-3,0] contains any divisor of 24. Line 2 and line 3 calculates a famous mathematical problem in ancient China and store the results within 500 in C1. The problem is known as Chinese Remainder Theorem, which asks: There are certain things whose number is unknown; if we count them by threes, we have two left over; by fives, we have three left over; and by sevens, two are left over; how many things are there? Here are results of A1, B1 and C1.

  

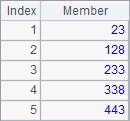
For a sequence having duplicate members, two aggregate functions A.count() and A.icount() can be used to perform two types of count. For example:

	A
1	[2,3,3,2,5,7,1]
2	=A1.count()
3	=A1.icount()

A2 counts the numbers of members in the given sequence, while A3 counts the number of its distinct members. Here are the results of A2 and A3:

 

We can use options in the function to increase computing efficiency. When all members of a sequence are integers, we add @n and the corresponding function is A.icount@n(); and when all members of a sequence are integers or long integers, we add @b and the corresponding functions is A.icount@b().

Some aggregate functions are order-related, like A.rank(y) function for data sorting and A.median(k:n) function for getting the median value.

	A	B	C
1	[6,8,1,3,7,2,4,9,5]
2	=A1.rank(8)	=A1.rank@z(8)
3	=A1.median()	=A1.median(1:4)	=A1.median(:3)

A2 finds the rank of 8 in A1 sequence in an ascending order. B2 find the member’s rank in a reversed order. Here are results of A2 and B2:

 

A3 finds the median in A1’s sequence. A median is the member with a value lying at the midpoint of a sequence. If the number of members in a sequence is even, the median is the average of the two members at the midpoint. Using certain parameters, the median() function can get the member at the segmenting point specified by the parameters in an ascending order. If the segmenting point falls between two members, the function will return the average of the two members. B3 gets the member at the 1/4 length of the sequence. In A.median(k:n) function, the number of segments n must be an integer not less than 2 and k must be an integer not greater than n. When parameter k is absent, the function returns values at the points where the sequence is divided evenly into n segments. Here are results of A3, B3 and C3:

  

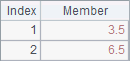
There are some functions for performing aggregation over multiple sequences. For example:

	A	B
1	[[1,2,3],[3],[3,4],[6,5,3]]
2	=A1.conj()	=A1.union()
3	=A1.diff()	=A1.isect()

A given sequence over which A.conj(), A.union(), A.diff(), A.isect() functions are performing operations needs to be a sequences whose members are also sequences. A2, B2, A3 and B3 compute the concatenation, union, difference and intersection of A1’s member sequences. Their results are as follows:

 

 

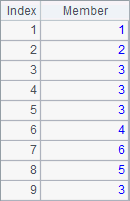
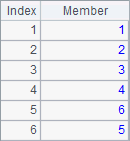
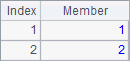
Loop functions

Loop functions perform same computation on each member of a sequence. The complex loop statements can be replaced by the simple loop functions which cover loop operation, filter, locate, query, rank and sort, etc. For example:

	A	B	C
1	[2,4,-6]	=A1.(~+1)
2	=A1.select(~>1)	=A1.pselect@a(~>1)	=A1.pos([-6,2])
3	=A1.ranks@z()	=A1.sort()	=A1.-sort(~)

B1 adds 1 to each member of the sequence. The resulting sequence is as follows:

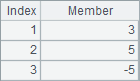
A2 selects members that are greater than 1. B2 finds ordinal numbers of members that are greater than 1. C2 searches for ordinal numbers of member -6 and member 2 in sequence A1. The results of A2, B2 and C2 are as follows:

   

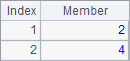
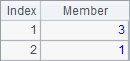
A3 uses @z option to get rankings of members in the sequence in a descending order. B3 sorts members of the sequence in ascending order, and C3 does it in descending order. The results of A3, B3 and C3 are as follows:

   

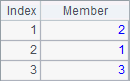
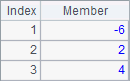
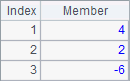
By the way, we can specify the starting and ending positions for the search in certain location functions. For example:

	A	B
1	[2,4,-6,null,4,3,]
2	=A1.pselect@a(~>1, 5)	=A1.pos(4,3)

A2 searches for positions of members greater than 1 starting from the 5^th member. B2 finds position of member 4 starting from the 3^rd member. Here are A2 and B2’s results:

 

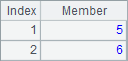
Besides @1 option and @z option, @0 is another option that often works with location functions. For example:

	A	B	C
1	[2,4,-6,null,4,3,]
2	=A1.pselect(~>10)	=A1.pselect@0(~>10)	=A1.pos(5)
3	=A1.pos@0(5)	=A1.pmin()	=A1.pmin@0()

After execution, A2, B2, C2, A3, B3 and C3 get their result as follows:

   

   

By working with @0 option, both A.pselect() function and A.pos() function returns 0 instead of null when they cannot find a corresponding member, and A.pmin@0() returns position of the first null value when there is one in the sequence. The @0 option can work with the some other location or select functions, including A.pfind(), A.ptop () and A.top().

In addition to @0 option, A.pselect() function and A.pos() function can also work with @n option to return “the length of the sequence plus 1” when a corresponding member cannot be found. For example:

	A	B
1	[2,4,-6,null,4,3,]
2	=A1.pselect@n(~>10)	=A1.pos@n(5)

Both A2 and B2 get same result:

 

Note that @0 option and @n option are mutually-exclusive. They cannot work together.